
한국외대 DSC(Developer Student Club) 멤버들과 함께 머신러닝 스터디를 진행하면서 “머신 러닝 교과서“를 블로그에 정리한 내용입니다.
로지스틱 회귀
로직스틱 회귀는 구현하기 매우 쉽고 선형적으로 구분되는 클래스에 뛰어난 성능을 내는 분류 모델입니다. 또한 다중 분류로도 확장할 수 있습니다. 예를 들어 OvR(One-versus-Rest)방식을 사용합니다.
먼저 오즈비(odds ratio)를 소개합니다. Odds는 특정 이벤트가 발생할 확률입니다. Odds ratio는 $\frac{P}{(1-P)}$처럼 쓸 수 있습니다. 여기서 $P$ 는 양성 샘플일 확률입니다. 양성 샘플은 좋은 것을 의미하지 않고 예측하려는 대상을 말합니다. 예를 들어 환자가 어떤 질병을 가지고 있을 확률입니다. Odds ratio에 로그 함수(log odds)를 취해 Logit 함수를 정의합니다.
\[logit(P) = log\frac{P}{(1-P)}\]여기서 $log$ 는 자연 로그 입니다. logit 함수는 0과 1 사이의 입력값을 받아 실수 범위 값으로 변환합니다. 특성의 가중치 합과 log odds 사이의 선형 관계를 다음과 같이 쓸 수 있습니다.
\[logit(P(y=1|x)) = w_0x_0+ w_1x_1+ ... + w_mx_m = \Sigma_{i=0}^mw_ix_i = w^Tx\]여기서 $p(y=1|x)$ 는 특성 x가 주어졌을 때 이 샘플이 클래스 1에 속할 조건부 확률입니다.
어떤 샘플이 특정 클래스에 속할 확률을 예측하는 것이 관심 대상이므로 logit 함수를 거꾸로 뒤집습니다. 이 함수를 로지스틱 시그모이드 함수(logistic sigmoid function)라고 합니다. 함수 모양이 S자 형태를 띠기 때문에 간단하게 줄여서 시그모이드 함수(sigmoid function)라고도 합니다.
\[\phi (z) = \frac{1}{1+e^{-z}}\]여기서 $z$ 는 가중치와 샘플 특성의 선형 조합으로 이루어진 최종 입력입니다. 즉, $z=w^Tx=w_0x_0+w_1x_1+…+w_mx_m$ 입니다.
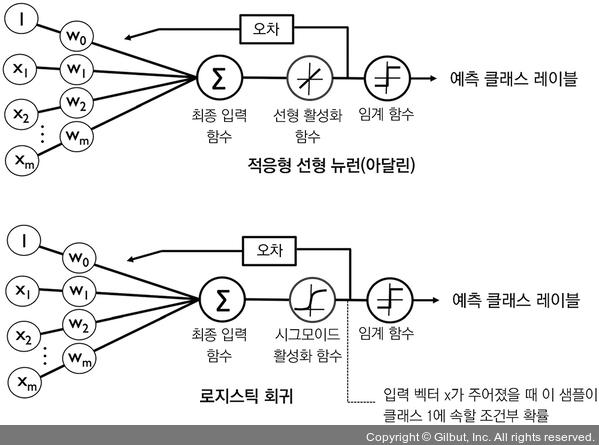
로지스틱 회귀 모델을 직관적으로 이해하기 위해 2장과 연관 지어 생각해 보겠습니다. 아달린에서 활성화 함수로 항등 함수 $\phi(z)=z$ 를 사용했습니다. 로지스틱 회귀에서는 앞서 정의한 시그모이드 함수가 활성화 함수가 됩니다. 아달린과 로지스틱 회귀의 차이점을 아래 그림에 나타냈습니다.
로지스틱 비용 함수(cost function)의 가중치 학습
이전 장에서 정의한 제곱 오차합 비용 함수는 아래와 같습니다.
\[J(w)=\Sigma_i\frac{1}{2}(\phi(z^{(i)}-y^{(i)})^2\]로지스틱 회귀의 비용 함수를 유도하는 방법을 설명하기 위해 먼저 로지스틱 회귀 모델을 만들 때 최대화하려는 가능도(likelihood) $L$ 을 정의하겠습니다. 데이터셋에 있는 각 샘플이 서로 독립적이라고 가정합니다. 공식은 다음과 같습니다.
\[L(w) = p(y|x;w) = \Pi_{i=1}^n(y^{(i)}|x^{(i)};w)=\Pi_{i=1}^n(\phi(z^{(i)}))^{y^{(i)}}(1-\phi(z^{(i)}))^{1-y^{(i)}}\]실전에서는 이 공식의 (자연)로그를 최대화하는 것이 더 쉽습니다, 이 함수를 로그 가능도(log likelihood) 함수라고 합니다.
\[l(w) = logL(w)=\Sigma_{i=1}^n[y^ilog(\phi(z^i))+(1-y^i)log(1-\phi(z^i))]\]첫째 로그 함수를 적용하면 가능도가 매우 작을 때 일어나는 수치상의 언더플로(underflow)를 미연에 방지합니다. 둘째, 계수의 곱을 계수의 합으로 바꿀 수 있습니다. 미적분을 기억하고 있을지 모르지만 이렇게 하면 도함수를 구하기 쉽습니다.
아달린 구현을 로지스틱 회귀(logistic regression) 알고리즘으로 변경
아달린 구현에서 비용 함수 $J$ 를 새로운 비용 함수로 바꾸기만 하면 됩니다.
\[J(w) = -\Sigma_i[y^ilog(\phi(z^i))+(1-y^i)log(1-\phi(z^i))]\]이 함수로 epoch마다 모든 훈련 샘플을 분류하는 비용을 계산합니다. 선형 활성화 함수를 sigmoid 활성화로 바꾸고 임계 함수가 클래스 레이블 -1과 1이 아니고 0과 1을 반환하도록 변경합니다. 아달린 코드에 이 세 가지를 반영하면 로지스틱 회귀 모델을 얻을 수 있습니다. 결과 코드는 다음과 같습니다.
class LogisticRegressionGD(object):
"""경사 하강법을 사용한 로지스틱 회귀 분류기
매개변수
------------
eta : float
학습률 (0.0과 1.0 사이)
n_iter : int
훈련 데이터셋 반복 횟수
random_state : int
가중치 무작위 초기화를 위한 난수 생성기 시드
속성
-----------
w_ : 1d-array
학습된 가중치
cost_ : list
에포크마다 누적된 로지스틱 비용 함수 값
"""
def __init__(self, eta=0.05, n_iter=100, random_state=1):
self.eta = eta
self.n_iter = n_iter
self.random_state = random_state
def fit(self, X, y):
"""훈련 데이터 학습
매개변수
----------
X : {array-like}, shape = [n_samples, n_features]
n_samples 개의 샘플과 n_features 개의 특성으로 이루어진 훈련 데이터
y : array-like, shape = [n_samples]
타깃값
반환값
-------
self : object
"""
rgen = np.random.RandomState(self.random_state)
self.w_ = rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
net_input = self.net_input(X)
output = self.activation(net_input)
errors = (y - output)
self.w_[1:] += self.eta * X.T.dot(errors)
self.w_[0] += self.eta * errors.sum()
# 오차 제곱합 대신 로지스틱 비용을 계산합니다.
cost = -y.dot(np.log(output)) - ((1 - y).dot(np.log(1 - output)))
self.cost_.append(cost)
return self
def net_input(self, X):
"""최종 입력 계산"""
return np.dot(X, self.w_[1:]) + self.w_[0]
def activation(self, z):
"""로지스틱 시그모이드 활성화 계산"""
return 1. / (1. + np.exp(-np.clip(z, -250, 250)))
def predict(self, X):
"""단위 계단 함수를 사용하여 클래스 레이블을 반환합니다"""
return np.where(self.net_input(X) >= 0.0, 1, 0)
# 다음과 동일합니다.
# return np.where(self.activation(self.net_input(X)) >= 0.5, 1, 0)
이 코드는 이진 분류 문제에만 적용할 수 있습니다. 아래는 붓꽃 데이터만 가지고 로지스틱 회귀 구현이 작동하는지 확인하는 코드입니다.
X_train_01_subset = X_train[(y_train == 0) | (y_train == 1)]
y_train_01_subset = y_train[(y_train == 0) | (y_train == 1)]
lrgd = LogisticRegressionGD(eta=0.05, n_iter=1000, random_state=1)
lrgd.fit(X_train_01_subset,
y_train_01_subset)
plot_decision_regions(X=X_train_01_subset,
y=y_train_01_subset,
classifier=lrgd)
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()