
한국외대 DSC(Developer Student Club) 멤버들과 함께 머신러닝 스터디를 진행하면서 “머신 러닝 교과서“를 블로그에 정리한 내용입니다.
Scikit-learn LogisticRegression 클래스 사용하기
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(solver='liblinear', multi_class='auto', C=100.0, random_state=1)
lr.fit(X_train_std, y_train)
plot_decision_regions(X_combined_std, y_combined,
classifier=lr, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
훈련된 Linear Regression 모델을 통해 값을 예측하면 다음과 같은 결과를 얻을 수 있습니다.
In [17]:
lr.predict_proba(X_test_std[:3, :])
Out[17]:
# 각 열의 합은 1입니다.
array([[3.17983737e-08, 1.44886616e-01, 8.55113353e-01],
[8.33962295e-01, 1.66037705e-01, 4.55557009e-12],
[8.48762934e-01, 1.51237066e-01, 4.63166788e-13]])
In [18]:
lr.predict_proba(X_test_std[:3, :]).sum(axis=1)
Out[18]:
# 각 열의 합이 1임을 보여줍니다.
array([1., 1., 1.])
In [19]:
lr.predict_proba(X_test_std[:3, :]).argmax(axis=1)
Out[19]:
# 최댓값을 가진 인덱스를 출력했습니다.
array([2, 0, 0])
In [20]:
lr.predict(X_test_std[:3, :])
Out[20]:
# 직접 predict 함수를 사용해서 예측할 수 있습니다.
array([2, 0, 0])
규제를 사용하여 과대적합 피하기
- 과대적합: 훈련 데이터에서는 잘 동작하지만 본 적 없는 데이터(테스트 데이터)로는 잘 일반화되지 않는 현상
- 과소적합: 훈련 데이터에 있는 패턴을 감지할 정도로 충분히 모델이 복잡하지 않다는 것을 의미합니다.
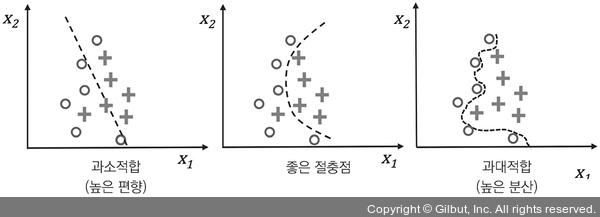
규제(Regularization)는 공선성(colinearity)(특성 간의 높은 상관관계)을 다루거나 데이터에서 잡음을 제거하여 과대 적합을 방지할 수 있는 매우 유용한 방법입니다. 규제는 과도한 파라미터(가중치) 값을 제한하기 위해 추가적인 정보(편향)를 주입하는 개념입니다. 가장 널리 사용하는 규제 형태는 다음과 같은 L2 규제입니다.
\[\frac{\lambda}{2}||w||^2 = \frac{\lambda}{2}\Sigma_{j=1}^mw_j^2\]로지스틱 회귀의 비용 함수는 규제 항을 추가해서 규제를 적용합니다. 규제 항은 모델 훈련 과정에서 가중치를 줄이는 역할을 합니다.
\[J(w) = -\Sigma_i[y^ilog(\phi(z^i))+(1-y^i)log(1-\phi(z^i))] + \frac{\lambda}{2}||w||^2\]규제 하이퍼 파라미터 $\lambda$ 를 사용하여 가중치를 작게 유지하면서 훈련 데이터에 얼마나 잘 맞출지를 조어할 수 있습니다. $\lambda$ 값을 증가하면 규제 강도가 높아집니다.