
한국외대 DSC(Developer Student Club) 멤버들과 함께 머신러닝 스터디를 진행하면서 “머신 러닝 교과서“를 블로그에 정리한 내용이다.
2장에서는 분류를 위한 초창기 머신 러닝 알고리즘인 퍼셉트론과 적응형 선형 뉴런 두개를 사용한다. 이 두 알고리즘에 대해 이해하고, 파이썬을 사용한 효율적인 구현 방법을 익히는데 도움이 될 것이라고 한다. 아래 3가지를 2장에서 주로 다룬다고 한다.
- 머신 러닝 알고리즘을 직관적으로 이해하기
- Pandas, Numpy, Matplotlib으로 데이터를 읽고 처리하고 시각화하기
- 파이썬으로 선형 분류 알고리즘 구현하기
적응형 선형 뉴런(ADAptive LInear NEuron, ADALINE)
퍼셉트론 알고리즘이 등장한 지 몇 년이 되지 지나지 않아 버나드 위드로우(Bernard Widrow)와 그의 박사 과정 학생 테드 호프(Tedd Hoff)가 아달린(Adaline)을 발표했다. 아달린은 퍼셉트론의 향상된 버전으로 볼 수 있다.
아달린은 연속 함수(continuous function)로 비용 함수를 정의하고 최소화 한다.
아달린 규칙(위드로우-호프 규칙이라고도 함)과 로젠블라트 퍼셉트론의 가장 큰 차이점은 가중치를 업데이트하는 데 퍼셉트론처럼 단위 계단 함수 대신 선형 활성화 함수를 사용한다는 것이다. 선형 활성화 함수 $\phi(z)$ 는 최종 입력과 동일한 함수이다.
\[\phi(w^Tx)=w^Tx\]하지만 최종 예측은 임계 함수를 사용한다.
퍼셉트론과 아달린 알고리즘의 비교
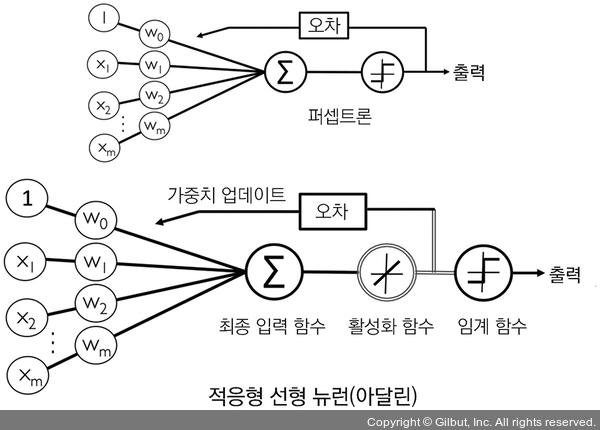
출처: https://thebook.io/007022/ch02/03-01/
오차 계산과 가중치 업데이트하는 방법
- 아달린 알고리즘: 진짜 클래스 레이블과 선형 활성화 함수의 실수 출력 값을 비교
- 퍼셉트론 알고리즘: 진짜 클래스 레이블과 예측 클래스 레이블과 비교
경사 하강법으로 비용 함수 최소화
목적 함수는 지도 학습 알고리즘의 핵심 구성 요소로 학습 과정 동안 최적화하기 위해 정의된다. 종종 최소화하려는 비용 함수가 목적 함수가 된다. 아달린은 제곱 오차함(Sum of Squared Errors, SSE)로 가중치를 학습할 비용 함수 $J$를 정의한다.
\[J(w) = {\frac{1}{2}}{\Sigma}_i(y^{(i)}-\phi(z^{i}))^2\]$\frac{1}{2}$ 항은 미분식을 간소하게 만들려고 편의상 추가한 것이다. 단위 계단 함수와 다르게 연속 함수는 미분 가능하다는 특징을 갖고 있다. 아래의 그림은 경사 하강법의 핵심 아이디어를 묘사한다.
경사 하강법 알고리즘
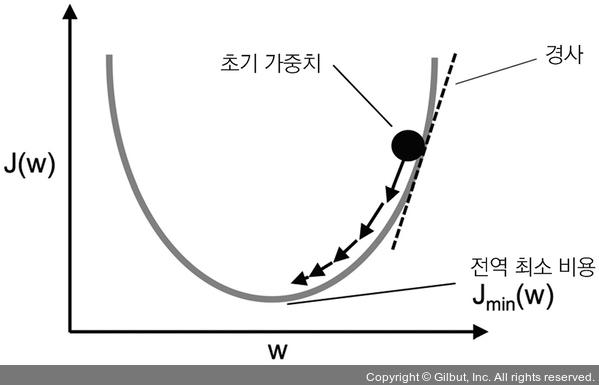
출처: https://thebook.io/007022/ch02/03/01/
수학적 그래디언트와 미분값은 구분된다. 수학적 표현으로 기울기를 $\nabla$ (gradient)라고 표현한다. 여기서 gradient는 스칼라를 벡터로 미분한 것이다.
경사 하강법은 아래와 같이 n번의 스텝을 통해 가중치를 업데이트 한다. $\alpha$ 는 학습률을 의미한다.
1-D의 경우
\[x_n = x_{n-1} - \alpha\frac{df(x_{n-1})}{dx}\]N-D의 경우
\[x_n = x_{n-1}-\alpha\nabla f(x_{n-1})\]아달린 학습 규칙이 퍼셉트론 규칙과 동일하게 보이지만 $z^{(i)}=w^Tx^{(i)}$인 $\phi(z^{(i)})$ 는 정수 클래스 레이블이 아니고 실수이다. 또 훈련 세트에 있는 모든 샘플을 기반으로 가중치 업데이트를 계산한다.(각 샘플마다 가중치를 업데이트 하지 않는다.) 이 방식을 배치 경사 하강법(batch gradient descent) 이라고 한다.
파이썬으로 아달린 구현
앞서 정의한 퍼셉트론 구현과 매우 비슷하고, fit 메서드만 바꾸어 경사 하강법으로 비용 함수가 최소화되도록 가중치를 업데이트 했다.
class AdalineGD(object):
"""적응형 선형 뉴런 분류기
매개변수
------------
eta : float
학습률 (0.0과 1.0 사이)
n_iter : int
훈련 데이터셋 반복 횟수
random_state : int
가중치 무작위 초기화를 위한 난수 생성기 시드
속성
-----------
w_ : 1d-array
학습된 가중치
cost_ : list
에포크마다 누적된 비용 함수의 제곱합
"""
def __init__(self, eta=0.01, n_iter=50, random_state=1):
self.eta = eta
self.n_iter = n_iter
self.random_state = random_state
def fit(self, X, y):
"""훈련 데이터 학습
매개변수
----------
X : {array-like}, shape = [n_samples, n_features]
n_samples 개의 샘플과 n_features 개의 특성으로 이루어진 훈련 데이터
y : array-like, shape = [n_samples]
타깃값
반환값
-------
self : object
"""
rgen = np.random.RandomState(self.random_state)
self.w_ = rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
net_input = self.net_input(X)
# Please note that the "activation" method has no effect
# in the code since it is simply an identity function. We
# could write `output = self.net_input(X)` directly instead.
# The purpose of the activation is more conceptual, i.e.,
# in the case of logistic regression (as we will see later),
# we could change it to
# a sigmoid function to implement a logistic regression classifier.
output = self.activation(net_input)
errors = (y - output)
self.w_[1:] += self.eta * X.T.dot(errors)
self.w_[0] += self.eta * errors.sum()
cost = (errors**2).sum() / 2.0
self.cost_.append(cost)
print(cost)
return self
def net_input(self, X):
"""최종 입력 계산"""
return np.dot(X, self.w_[1:]) + self.w_[0]
def activation(self, X):
"""선형 활성화 계산"""
return X
def predict(self, X):
"""단위 계단 함수를 사용하여 클래스 레이블을 반환합니다"""
return np.where(self.activation(self.net_input(X)) >= 0.0, 1, -1)
위의 코드는 UCI 머신 러닝 저장소의 붓꽃 데이터를 다루기 위한 코드다.
- activation 메서드는 단순 항등 함수(identity function)이다. 아무런 영향을 끼치지 않는다.
- 입력 데이터의 특성에서 최종 입력, 활성화, 출력 순으로 진행 된다.
특성 스케일을 조정하여 경사 하강법 결과 향상
책에서 소개하는 알고리즘들은 최적의 성능을 위해 특성 스케일이 필요하다. 경사 하강법은 여러 특성 스케일을 조정하는 알고리즘 중 하나이다. 여기서 소개할 방법은 표준화(standardization)이다. 아래는 $j$ 번째 특성을 표준화 하기 위해 모든 샘플에서 $\mu_j$ 를 빼고 표준 편차 $\sigma_j$ 로 나눈 것이다.
\[x^{'}_j = \frac{x_j-\mu_j}{\sigma_j}\]여기서 $x_j$는 $n$개의 모든 훈련 샘플에서 $j$ 번째 특성 값을 포함한 벡터이다. 아래는 표준화가 경사 하강법 학습에 도움이 되는 이유를 나타낸다.
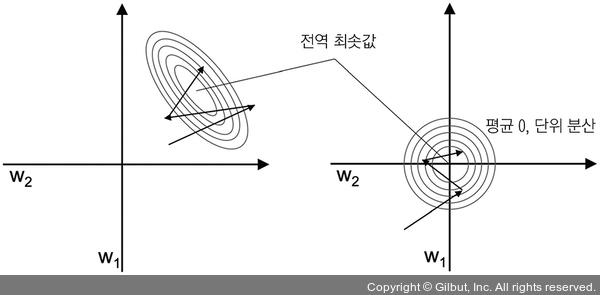
numpy에서는 내장 함수 mean과 std로 간단하게 처리할 수 있다.
# 특성을 표준화합니다.
X_std = np.copy(X)
X_std[:, 0] = (X[:, 0] - X[:, 0].mean()) / X[:, 0].std()
X_std[:, 1] = (X[:, 1] - X[:, 1].mean()) / X[:, 1].std()
대규모 머신 러닝과 확률적 경사 하강법
이전에 배운 배치 경사 하강법을 사용하면 수백만 개의 데이터 포인트가 있는 큰 데이터셋에서는 계산 비용이 매우 많이 든다는 단점이 있다.
확률적 경사 하강법(stochastic gradient descent)은 배치 경사 하강법의 다른 대안으로 인기가 높다.
- 장점: 비선형 비용 함수를 다룰 때 얕은 지역 최솟값을 더 쉽게 탈출할 수 있다.
- 단점: 그래디언트가 하나의 훈련 샘플을 기반으로 계산되므로 오차의 궤적은 배치 경사 하강법보다 훨씬 어지럽다.
만족스러운 결과를 위해 매 epoch마다 훈련 세트를 섞는 것이 좋다.
note: 적응적 학습률(adaptive learning rate)를 사용하면 최솟값에 더욱 가깝게 다가갈 수 있다. ($c_1$, $c_2$는 상수이다.) \(\frac{c_1}{[number of iterations]+c_2}\)
note: 배치 경사 하강법과 확률적 경사 하강법 사이의 절충점으로 미니 배치 학습(mini-batch learning)이 있다. 훈련 샘플의 일부분만을 학습에 사용하는 것이다.
파이썬으로 구현한 SGD
class AdalineSGD(object):
"""ADAptive LInear NEuron 분류기
Parameters
------------
eta : float
학습률 (0.0과 1.0 사이)
n_iter : int
훈련 데이터셋 반복 횟수
shuffle : bool (default: True)
True로 설정하면 같은 반복이 되지 않도록 에포크마다 훈련 데이터를 섞습니다
random_state : int
가중치 무작위 초기화를 위한 난수 생성기 시드
Attributes
-----------
w_ : 1d-array
학습된 가중치
cost_ : list
모든 훈련 샘플에 대해 에포크마다 누적된 평균 비용 함수의 제곱합
"""
def __init__(self, eta=0.01, n_iter=10, shuffle=True, random_state=None):
self.eta = eta
self.n_iter = n_iter
self.w_initialized = False
self.shuffle = shuffle
self.random_state = random_state
def fit(self, X, y):
"""훈련 데이터 학습
Parameters
----------
X : {array-like}, shape = [n_samples, n_features]
n_samples 개의 샘플과 n_features 개의 특성으로 이루어진 훈련 데이터
y : array-like, shape = [n_samples]
타깃 벡터
반환값
-------
self : object
"""
self._initialize_weights(X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
if self.shuffle:
X, y = self._shuffle(X, y)
cost = []
for xi, target in zip(X, y):
cost.append(self._update_weights(xi, target))
avg_cost = sum(cost) / len(y)
self.cost_.append(avg_cost)
return self
def partial_fit(self, X, y):
"""가중치를 다시 초기화하지 않고 훈련 데이터를 학습합니다"""
if not self.w_initialized:
self._initialize_weights(X.shape[1])
if y.ravel().shape[0] > 1:
for xi, target in zip(X, y):
self._update_weights(xi, target)
else:
self._update_weights(X, y)
return self
def _shuffle(self, X, y):
"""훈련 데이터를 섞습니다"""
r = self.rgen.permutation(len(y))
return X[r], y[r]
def _initialize_weights(self, m):
"""랜덤한 작은 수로 가중치를 초기화합니다"""
self.rgen = np.random.RandomState(self.random_state)
self.w_ = self.rgen.normal(loc=0.0, scale=0.01, size=1 + m)
self.w_initialized = True
def _update_weights(self, xi, target):
"""아달린 학습 규칙을 적용하여 가중치를 업데이트합니다"""
output = self.activation(self.net_input(xi))
error = (target - output)
self.w_[1:] += self.eta * xi.dot(error)
self.w_[0] += self.eta * error
cost = 0.5 * error**2
return cost
def net_input(self, X):
"""최종 입력 계산"""
return np.dot(X, self.w_[1:]) + self.w_[0]
def activation(self, X):
"""선형 활성화 계산"""
return X
def predict(self, X):
"""단위 계단 함수를 사용하여 클래스 레이블을 반환합니다"""
return np.where(self.activation(self.net_input(X)) >= 0.0, 1, -1)
요약
지도 학습의 기초적인 선형 분류기 개념을 배웠다.